Oscillations
Learning objectives
- Understand the conditions under which simple harmonic oscillations take place.
-
Identify and use the concepts of period, frequency, amplitude, displacement and phase difference.
-
Describe simple harmonic oscillations graphically.
-
Describe the energy transformations taking place in oscillations.

Simple Harmonic Motion
Periodic Motion
- Oscillations refer to the back and forth motion of an object, such as a pendulum. In an oscillation, motion is repetitive or periodic, and the body moves back and forth around an equilibrium position. Simple harmonic motion is an example of periodic motion. A example of a periodic motion is a spring modeled by a sinusoidal function.

Figure 1: Image of a simple pendulum
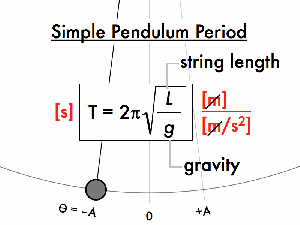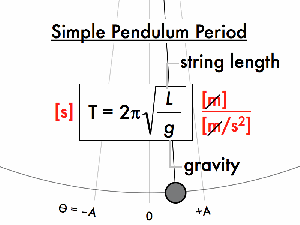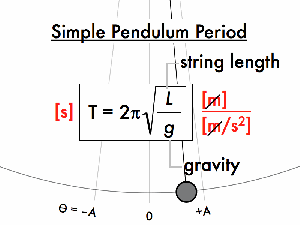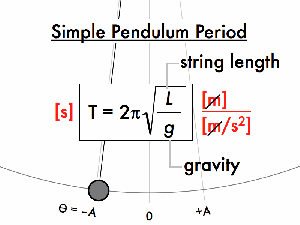


Oscillations and Function
Motion with oscillations can often be modeled by a sinusoidal function: trigonometric function of sine or cosine as demonstrated by two figures below. The modeled function is knows as a wave that has different features represented by mathematical symbols.

Figure 2: Structure and key terms of a wave

Figure 3: Equation of a sinusoidal function
Important Quantities of A Wave
- Crest and Trough: Crest is the highest point of a wave, and trough is the lowest point of a wave
- Wavelength: Wavelength is the distance between two adjacent crest or two neighborhood trough
- Amplitude: Amplitude is the distance between a wave's crest or trough to its sea level
- Frequency: frequency f of the oscillations as the number of full oscillations per second
- Period: The time it takes to complete one oscillation
- Phase shift
Energy in A Simple Harmonic Motion
- According to conservation of energy, the total energy of a system is conserved or remains constant. The total energy of a system is equal to the sum of kinetic energy and potential energy, ignoring the existence of friction.
- During a collision of simple harmonic motion, energy is transformed into different form. For example, when a spring is compressed in a mass-spring system, kinetic energy is transformed into spring potential energy. And at its maximum compression, object's has a velocity of zero, so the total energy is equal maximum spring potential energy.


