Gravitation
Understandings
- Newton’s law of gravitation
- Coulomb's law and gravitation
- Gravitational field strength
- Gravitational potential energy
- Centripetal force and gravitation

Four Fundamental Forces
In mechanics, we learned that the weight of an object near a planet's surface can be calculated by using the formula of W=mg. Before talking about Newton's law of universal gravitation, it is important to understand the four fundamental forces in physics, illustrated by the below image (figure 1).

Figure 1: Four fundamental forces
Newton's Law of Universal Gravity
- Newton's Law of Universal Gravitation states the force of gravity by a plane F is inversely proportional to distance squared.
- The formula of Newton's law of universal gravitational is similar to the formula of Coulomb's law

Figure 2: Newton's law of universal gravity equation and Coulomb's law
Gravitational Field Strength
The gravitational field strength at a certain point is the gravitational force per unit mass experienced by a small point mass m placed at that point. The gravitational field strength around a single point or spherical mass is radial, which means that it points towards the centre of the mass creating the field.


Figure 3/Equation1: Equation for gravitational field strength
From the equation of gravitational field strength, we can see that gravitational field strength is identical to an object's acceleration when it orbits around another object.
Orbital Motion
- For a planet in a circulation motion, its net force(centripetal force) is equal to its gravitational attraction force. From this relation, we can derive the formula of centripetal velocity (orbital velocity) of the object in circular motion.
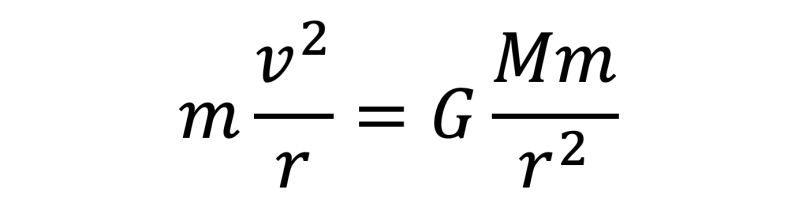
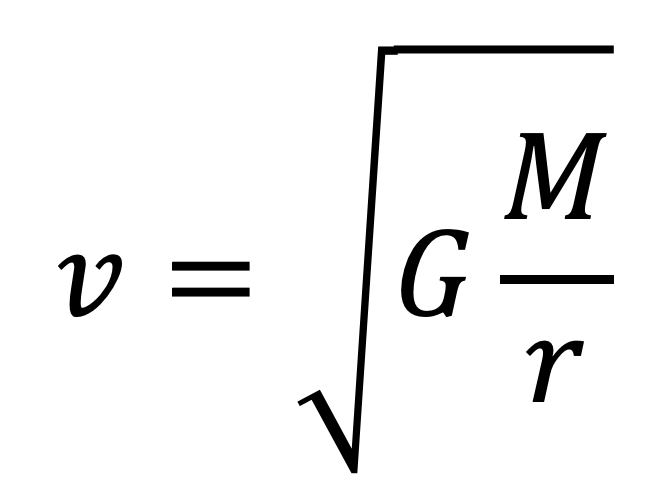
Equation 2: Orbital velocity of a planet
We know that velocity is equal to perimeter divided by time, and from this relationship we can derive another equation of period.



Equation 3: An object's period in circular motion
Conservation of Energy and Orbital Motion
In the topic of mechanics, we have introduced the theory of conservation of energy, stating that the total amount of energy of a system is conserved if there is no external forces acting on it.
Equation 1 derives the formula of an object's orbital velocity in circular motion. By combining the equation with conservation of energy, we are able to gain a more detailed picture of circular motion, shown by the equation below.


Equation 2: Conservation of energy for an object's in circular motion
To derive the equation, integral is required (Visit math background if you haven't learned calculus). In previous topics, we learnt that mgh can be used to calculate gravitational potential energy by assuming mg, weight as a constant. However, from Newton's law of universal gravity, we know that the force of gravitation varies with the distance between two objects.

Figure 6: Deriving the equation of gravitational potential energy by using integral

Equation 4: Initial gravitational potential energy
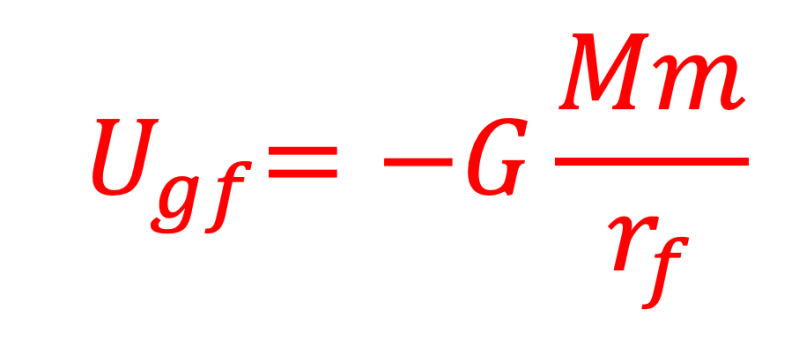
Equation 5: Initial gravitational potential energy
Gravitational Potential
The gravitational potential at a point in a gravitational field is the work done per unit mass that would be needed to move an object to that location from a fixed reference location. It is a scalar quantity that is assumed to equal to zero at infinity, so sit always remains negative.


Extension
- If you are interested in Newton's Law of gravitation and astrophysics, here are some interested theories and extension beyond the textbook. Those topics might be covered in the optional topic of astrophysics in IB and gravitation chapter in collage physics and AP physics.
- Kepler's law in polar forms
- Newton's generalization of Kepler's Law
- Tidal forces (How distance impacts the shape of objects)
Check Your Understand
Gravitational Quiz 1 - Easy
- Total Mark: 5 marks with no calculator
- Total Time: 8 minutes